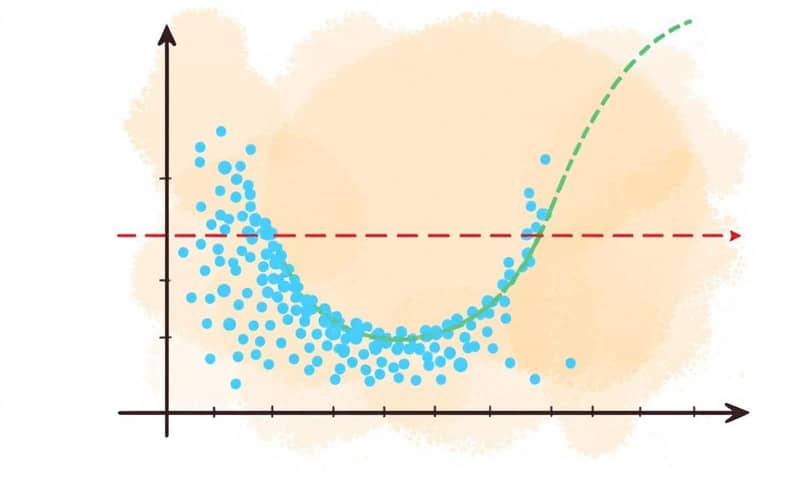
最近よく聞かれるのが、データに線を引く話。うん、回帰分析のこと。でも、いつも直線でいいかっていうと、そうでもないんだよね。むしろ、まっすぐな線じゃ全然ダメなことの方が多い。
データが、こう…ぐにゃっと曲がってる時。無理やり直線を引いても、全然フィットしない。当たり前だけど。そういう時に、じゃあどうすんの?って話。
重点一句話
要は、直線じゃなくて、データに合わせてグニャグニャ曲がる「曲線」を引くための方法が、この多項式回帰ってやつ。意外とシンプル。うん、でも奥が深い。
で、多項式回帰って結局なんなの?
名前はなんか難しそうだけど、やってることは線形回帰の拡張。うん、ただのバージョンアップみたいなもん。
普通の線形回帰って、`y = ax + b` みたいな、中学校で習う一次関数の式でしょ。だから直線しか引けない。
これを、`x` の2乗、3乗…っていう項(パーツ)を付け足していく感じ。`y = c*x^2 + a*x + b` みたいな。二次関数になると、もう放物線が描ける。こうやって「曲がり」を表現できるようになる。もっと複雑にしたければ、3乗、4乗と増やしていけばいい。それが多項式回帰。
あ、ちなみに日本の総務省統計局が出してる高齢化率のデータとか見ても、あれ、直線じゃ説明できないですよね。最初は緩やかで、途中からグッと上がっていく。ああいうのが、まさに曲線で捉えたいデータの典型例。
どの「次数」を選ぶかが、たぶん一番大事
コードを見る前に、まずこの問題にぶち当たる。次数、つまり `x` の何乗まで使うか、って話。これを間違えると、もう全然ダメなモデルになる。
ちょっと極端な例を見てみようか。わざと作った、こんな感じのデータがあるとして。

この図、すごく示唆的だと思う。うん。
- 次数1(直線): 話にならない。全然データの形を捉えられてない。これが「モデルが単純すぎてダメ」な例。アンダーフィットってやつ。
- 次数2(曲線): なかなかいい感じ。うん、データの大きな流れをうまく捉えてるように見える。
- 次数7(ぐにゃぐにゃの線): これは…やりすぎ。個々のデータ点を無理やり全部通ろうとして、結果的になんか不自然な形になってる。これが「モデルが複雑すぎてダメ」な例。過学習(オーバーフィッティング)。たぶん、新しいデータが来たら、このモデルは全然予測を当てられない。
つまり、ちょうどいい「曲がり具合」を見つけるのが、この手法のキモなんだよね。
じゃあ、どうやって選ぶの?っていう話
正直、一発で「これだ!」って見つける魔法はない。でも、考え方の指針みたいなものはある。僕がよくやるのは、こんな感じで頭の中を整理することかな。
| 次数 | 見た目・特徴 | リスク | 個人的な使いどころ |
|---|---|---|---|
| 低い次数 (1, 2) | 直線か、なめらかな放物線。シンプル。 | アンダーフィット。データの複雑さを見逃してるかも。 | まず最初に試す。だいたいの傾向を見るならこれで十分なことも多い。 |
| 中くらいの次数 (3-5) | S字カーブとか、もうちょっと複雑な形もいける。 | ちょうどいいかもしれないし、過学習の入り口かもしれない。微妙なライン。 | 2次で足りないな、と感じた時に少しずつ上げて試すゾーン。R2スコアとか見ながら慎重に。 |
| 高い次数 (6以上) | ぐにゃぐにゃ。訓練データに媚びすぎてる感じ。 | 過学習のリスクがめちゃくちゃ高い。ほぼ確実に、未知のデータには弱い。 | うーん…正直、よっぽどの理由がないと使わない。データの外側で予測が爆発するし。研究とかで、特定の現象を表現したい時くらい…? |
Pythonでゼロから作ってみる
理屈はなんとなくわかったとして、じゃあ実際にどうやって作るのか。ここでは `scikit-learn` みたいな便利なライブラリに頼らず、あえて自分で計算してみる。その方が、中で何が起きてるかわかるから。
ステップ1: 準備運動
まず、必要なものをいくつかインポートする。`numpy` は計算の鬼だし、`matplotlib` はグラフ描画の相棒。
import numpy as np
import matplotlib.pyplot as plt
# あとでモデルの評価に使う
from sklearn.metrics import r2_scoreステップ2: 実験用のデータを作る
さっき見せたみたいな、ちょっと曲線っぽいデータセットを人工的に作る。`y = 1.5*x^2 + 3*x + 2` みたいな式をベースに、わざとノイズ(`np.random.normal`)を加えて、ちょっと散らばった感じにする。現実のデータって、だいたいこんな感じだよね。
# いつやっても同じ結果になるように、乱数の種を固定
np.random.seed(42)
# 0から10までの数字を100個用意
X = np.linspace(0, 10, 100).reshape(-1, 1)
# ちょっと二次関数っぽいデータを作る
# 2 + 3*x + 1.5*x^2 にノイズを足す
y = 2 + 3*X.flatten() + 1.5*X.flatten()**2 + np.random.normal(0, 10, 100)
# どんなデータができたか、一応プロットして見てみる
plt.scatter(X, y, alpha=0.8)
plt.title("実験用のデータ")
plt.show()ステップ3: 特徴量を作る(x を x, x², x³... に変身させる)
ここが多項式回帰の「多項式」たる所以。もともと `x` しかなかった入力データを、`[1, x, x^2, x^3]` のようなセットに変換する関数を作る。`1` は切片(バイアス項)のため。これ、地味に大事。
def create_polynomial_features(X, degree):
# Xの行数に合わせて、degree+1個の列を持つ配列を準備。最初は全部1で埋めておく。
# [1, 1, 1, ...],
# [1, 1, 1, ...], ...
X_poly = np.ones((X.shape[0], degree + 1))
# 1乗からdegree乗まで、順番に計算して列を埋めていく
for i in range(1, degree + 1):
X_poly[:, i] = X.flatten() ** i
return X_poly
# とりあえず3次で作ってみるか
degree = 3
X_poly = create_polynomial_features(X, degree)
# 変換後の最初の3行だけ見てみる
# [1, x, x^2, x^3] の形になってるはず
print(X_poly[:3])ステップ4: 係数を見つける(最小二乗法)
さて、`y = c*x^2 + a*x + b` の `a, b, c` にあたる「最適な係数」を見つけたい。一番それっぽい線を引くための数字。これを計算で一発で求めるのが、最小二乗法。なんか難しい数式 `β = (X^T X)^(-1) X^T y` が出てくるけど…
これは、要するに「予測と実際のデータの誤差(の2乗の合計)が、一番小さくなるような係数βを見つける魔法の呪文」だと思えばいい。`numpy` を使えば、この計算も数行で書ける。

def least_squares_fit(X_poly, y):
# ここが魔法の呪文の部分
# (X^T * X)^-1 * X^T * y
# X_poly.T.dot(X_poly) は Xの転置行列とXの積
# np.linalg.inv() は逆行列を計算
XTX_inv = np.linalg.inv(X_poly.T.dot(X_poly))
# X_poly.T.dot(y) は Xの転置行列とyの積
XTy = X_poly.T.dot(y)
# 最後にそれらを掛け合わせる
coeffs = XTX_inv.dot(XTy)
return coeffs
# 実際に計算してみる
coefficients = least_squares_fit(X_poly, y)
print("見つかった係数:", coefficients)
# 出てきた係数は [b, a, c, d] ... の順番に対応するはず
# [定数項, xの係数, x^2の係数, x^3の係数]ステップ5: 予測して、評価する
係数がわかれば、あとは新しい`X`を入れて予測値`y_pred`を計算するだけ。で、その予測がどれくらいいい感じか、R2スコア(決定係数)で評価する。1に近いほど、よく説明できてるってこと。
def predict(X_poly, coefficients):
# 行列の積を計算するだけ。シンプル。
return X_poly.dot(coefficients)
# 予測値を計算
y_pred = predict(X_poly, coefficients)
# R2スコアを計算
r2 = r2_score(y, y_pred)
print(f"R2スコア: {r2:.4f}")R2スコア、0.98超えか。かなり良い感じ。うん、3次でだいたい説明できてるみたいだね。
まとめ、というか気をつけること
多項式回帰、便利だよね。うん、直線じゃダメな時に、すぐ使えるカードになる。でも、やっぱり怖いのは「過学習」。さっきの次数7の例みたいに。
モデルを複雑にしすぎると、手元のデータには完璧にフィットするけど、未知のデータが来た瞬間に全く役に立たない「内弁慶」なモデルが出来上がってしまう。これを避けるためには、
- データを訓練用とテスト用に分ける。これは基本中の基本。
- 高い次数を使うなら、Ridge回帰とかLasso回帰みたいな「正則化」を検討する。係数が大きくなりすぎるのを防いでくれる。
- 交差検証(クロスバリデーション)で、どの次数が一番安定して良い性能を出すかチェックする。
結局、一番大事なのは「やりすぎない」こと。シンプルなモデルで説明できるなら、それに越したことはない。複雑にするのは、本当にそれが必要な時だけ。うん、たぶん、それが一番言いたいことかな。
あなたの扱ってるデータで、曲線っぽい関係性って何かありますか?もしよかったら、どんなデータで試してみたいか、教えてくれると嬉しいです。